크루스칼 알고리즘은 가장 적은 비용으로 모든 노드를 연결하여 최소비용신장트리를 만들 때 사용하는 알고리즘이다.

가장 가중치가 작은 간선부터 골라가는 그리디한 방법이며 작동과정 중 사이클이 생기지 않도록 유니온파인드를 사용해 해결한다.

• 깊이 우선 탐색(Depth First Search)
  • 루트 노드에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
  • 재귀함수를 기반으로 순환 알고리즘의 형태를 지님.
    
• 너비 우선 탐색(Breath First Search)
  • 루트 노드에서 시작해서 인접한 노드를 먼저 탐색하는 방법
  • 재귀함수로 동작하지 않는다.
  • 큐를 사용하여 효율적으로 구현 가능하다.

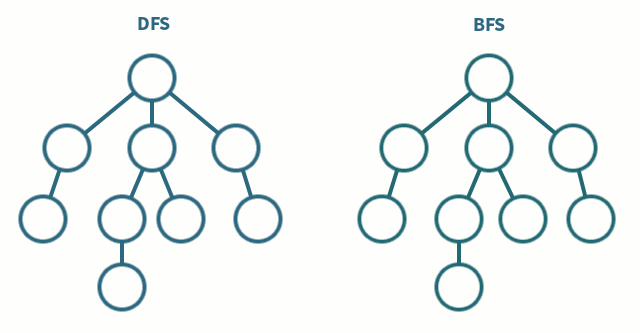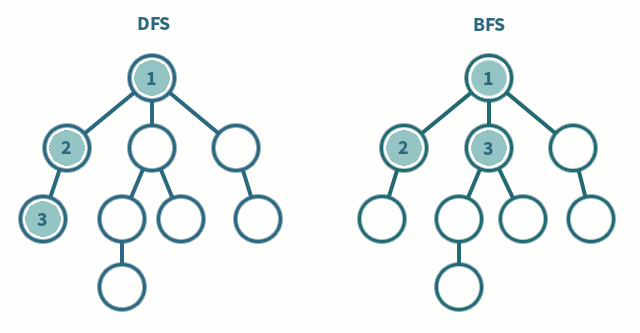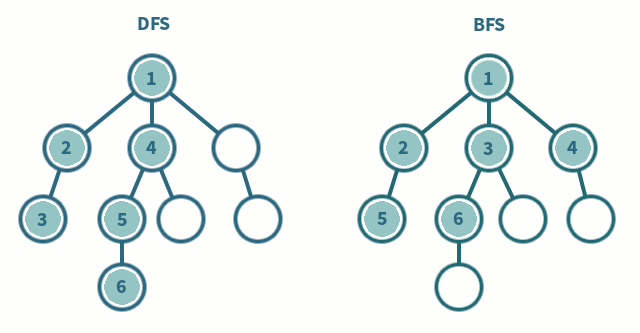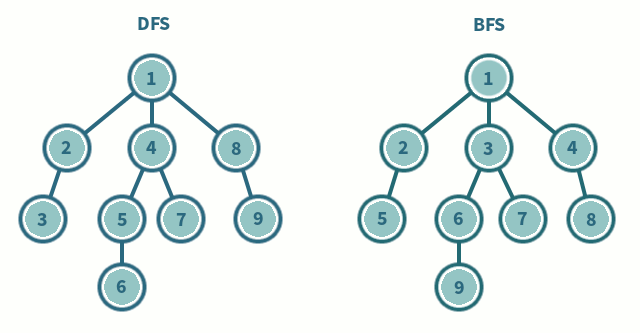
스택과 큐는 선형구조로 분류되는 자료구조 중 대표적인 예시이다.

처음엔 무식하게 2중 for문으로 돌려보았다.
맞겠지 싶었는데 시간초과가 떴다.

내가 만들고 싶은건 아니고 부탁받았다.
내용은 아래와 같다.

• 팀은 월 화 수 목 금
• 세션은 보컬 신디 베이스 기타 드럼
• 각 팀마다 세션에 들어가는 인원이 최소 한 명 이상은 있어야 함
• 팀의 특정 세션의 최소, 최대 인원수를 정하고 돌릴 수 있으면 좋겠음
• ex) 월요일팀 보컬 1~2 기타 1~3 베이스 2 신디 2~3 드럼 2
• 이름, 가능한 세션(복수선택 가능), 가능한요일(복수선택 가능), 희망하는 최대 팀 개수를 입력
• 팀을 짤 때 둘 이상의 세션에 한 사람만 들어가면 안됨
• ex) 보컬 A, 기타 A, 신디 B, 베이스 C, 드럼 D
• 희망하는 최대 팀 개수가 2 이상인 사람을 팀에 그보다 적게 넣어도 팀이 짜진다면 굳이 더 넣을 필요 없음
• 꼭 한 팀에 붙어야 되는 사람을 정할 수 있으면 좋겠음 (희망사항ㅎㅎ)
• ex) E랑 F는 꼭 같은 팀이어야 한다.

이전의 반도체 설계 문제와 동일하게 최장 증가 수열을 구하는 문제다.

2020년 4원 7일 포스트 수정

저 문제 풀 때는 dp가 뭔지도 몰랐다.
이번엔 동적 계획법으로 풀어봤다.
dp[i]에 arr[i]이전의 값들을 비교하며 arr[i]보다 작은 값이 있다면 그 때의 dp[]에 담겨있는 값 + 1을 dp[i]에 넣는다. arr[i]이전의 모든 수에 위 과정을 반복했을 때 가장 큰 수가 dp[i]가 된다.
마지막으로 dp[]에 담겨있는 값 중 가장 큰 값이 최장증가수열의 길이가 된다.

뭔가 했는데 알고리즘 분류를 보니 LIS라고 한다.

lower_bound로 최장증가수열을 구현하는 방식을 봤는데 실제로 유효한 수열을 구하진 않았다.

그런데 이 문제는 수열을 구하는 게 아니라 수열의 길이만 구하면 되므로 최대한 생략하고 수열의 길이만 구하도록 바꿨다.

1. 짝수 번 선택시 원래대로가 되기 때문에 같은 칸을 두 번 이상 선택할 필요가 없다.

2. 1번 조건을 다르게 생각해보면 선택 순서또한 중요치 않다는 뜻도 된다.

왼쪽 위부터 한자리씩 비교하며 다르면 그 칸을 포함해 오른쪽으로 3, 아래로 3 칸을 바꿔준다.

전체가 같아지면 멈추고 모든 칸을 다 바꿨는데 다르면 -1출력.

가장 큰 수를 구할 때

1. 앞자리에 9를 넣고 시작한다.

2. 다음 부등호가 “<” 라면 부등호 다음 수를 9로 만들고 그전의 자리에는 -1을 해준다.

3. “>” 라면 사용 안 했던 수 중에 가장 큰 수를 넣는다.
   이런 방식으로 부등호 개수만큼 반복한다.

딴 거 다 필요 없고 가장 싼 패키지와 낱개 가격만 있으면 된다.

그걸 구하기 위해 나는 정렬을 사용한 모양이다. 굳이 그랬어야 할까.

아무튼 경우의 수는 3가지다.

1. 패키지로 살 수 있을 만큼 산 후 나머지 부족한 것을 낱개로 구입.

2. 전부 낱개로 구입.

3. 기타줄 몇 개 남더라도 싹 다 패키지로 구입.

3개 중 가장 작은 게 답이다.