[C++]BOJ 2167 - 2차원 배열의 합

그리디로 풀었을 때 최악의 경우 n * m * k번, 300 * 300 * 10,000 = 900,000,000번 계산하므로 시간초과가 난다.
그래서 dp로 풀어야 한다. 할 줄 알았는데 그리디하게 풀어도 맞는다고 한다.

어쨌든 dp[i][j] 에는 (0, 0)부터 (i, j) 까지의 숫자 합을 저장한다.

dp[][] 를 채워나가는 방법

---

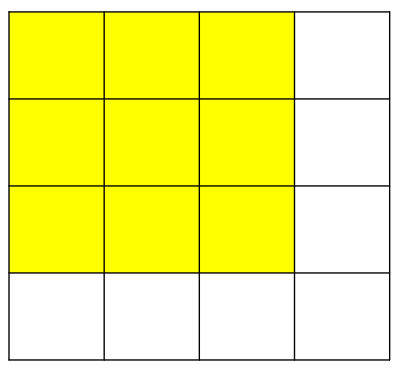
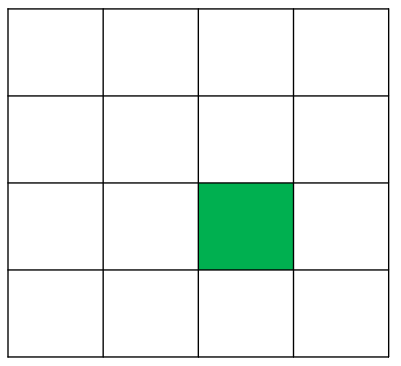
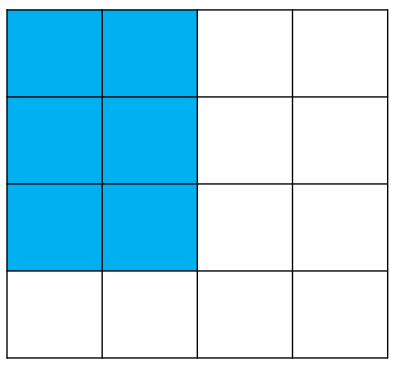
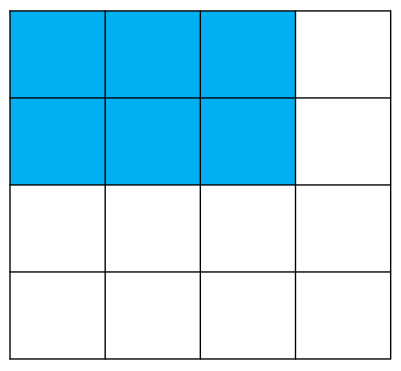
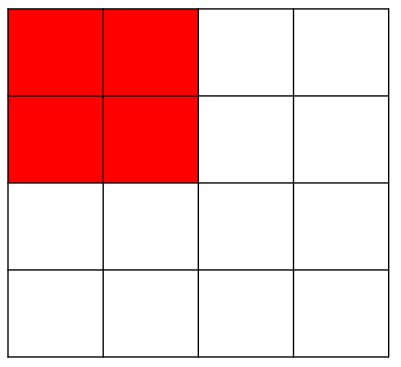
주어진 영역의 합을 구하는 방법

---

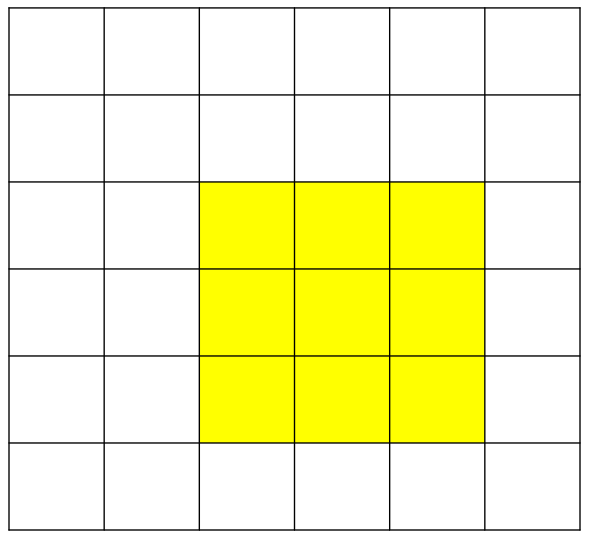
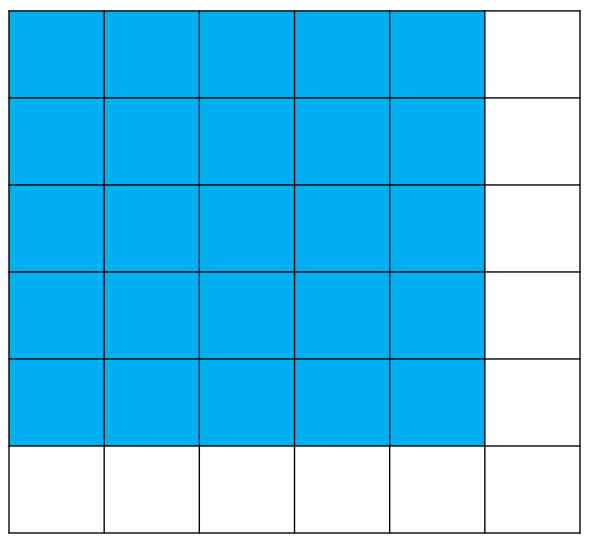
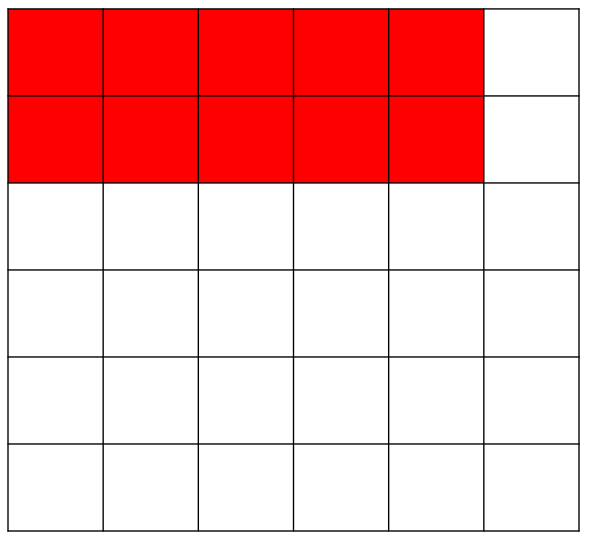
위 과정을 코드로 작성하면 아래와 같다.

#include <iostream>
using namespace std;
int n, m, ans, i, j, x, y, dp[301][301];
int main() {
	cin >> n >> m;
	for(i = 1; i <= n; i++)
		for(j = 1; j <= m; j++) {
			cin >> dp[i][j];
			dp[i][j] += dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
		}
	cin >> n;
	for(int k = 0; k < n; k++) {
		cin >> i >> j >> x >> y;
		ans = dp[x][y] - dp[x][j - 1] - dp[i - 1][y] + dp[i - 1][j - 1];
		cout << ans << endl;
	}
}